Have you heard of the Phong shader? A shader is a small function or program that determines the color of each individual pixel in a computer-generated image. Gouraud’s 1971 shader is one of the simplest, both to understand and to implement. In 1975, along comes Bui Tuong Phong and completely changes the game. (Well, Wikipedia says he first published his algorithm in 1973, in his Ph.D. thesis.)
The figure on the left above uses a flat polygon shader by Newell, Newell and Sancha. Each polygon has a uniform brightness to it, a technique known as flat shading. The figure on the right uses Phong's new shader. The difference is incredible, isn't it? For the one on the left, you would think either that the vase is itself faceted, or that it's reflecting rectangles such as windows. The one on the right is much more natural.
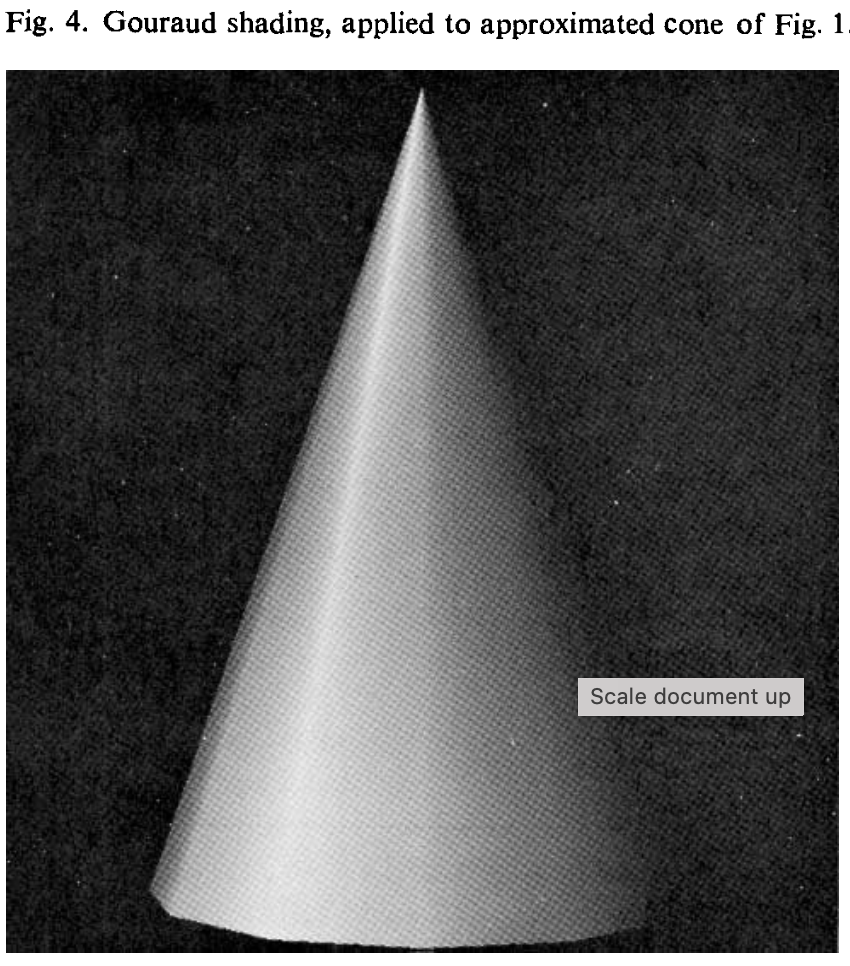
Gouraud's shader doesn't flat-shade each polygon. It begins with the set of normal vectors for each polygon, then it finds the normal at each vertex by averaging the normals of the surrounding polygons, a clever idea. Then it interpolates linearly along each edge. Finally, when creating the pixels in each scan line, it looks left and right from each pixel to find the nearest edge in each direction, and linearly interpolates from there. I'm a little surprised this works with polygons that are rather skewed, but if you think about it it's generally fine.
The problem arises because the interpolation is smooth within the polygon, but the slope of that interpolation has a discontinuity where you cross boundaries. This results in an effect known as Mach bands, where the human visual system assigns a ridge of brightness just to one side of that discontinuity, visible in the figure on the left below (or in the first figure if your browser shows them stacked).
Most importantly, in Gouraud shading, the values for the pixels are linearly interpolated. With Phong shading, instead, normal vectors are interpolated. Once you have the normal vector for the point, you can then calculate the appropriate projections to determine specular reflection as well as actual value. This means calculating cosines, or approximations of them, and taking square roots. It's a lot more math than Gouraud, but the quality of the results in the figure on the right above is obvious. This comes largely due to the now continuous first derivative as you cross polygon boundaries.
Oh, and a historical note: I mentioned in the 1974 spelunking that Utah was (and is) an important proving ground in computer graphics. Guess what? Both Gouraud and Phong were at the University of Utah. And, sadly, Phong died very young, of leukemia, indeed right after publishing this paper.
In looking to the future, it will be interesting to observe whether or not the number of women graduates increases in the fields related to computer design and use. It will be even more interesting to see if the percentages of women in the higher levels of programming and systems analysis increase as the women now in the lower levels gain experience and become eligible for promotion... For the present, the conclusion must be reached that there is still a long way to go before the statistics will indicate that women enjoy complete equality with men in the computer field.
Guy Steele himself wrote a long paper on garbage collection using a shared-memory multiprocessor. Very forward thinking. I'm actually a little surprised at the complexity of this.
Overall, to me, 1975 was a much quieter year than the explosive year of 1974.





No comments:
Post a Comment